Science
How String Theory Unraveled Math’s Monstrous Moonshine Enigma
An idea originating from theoretical physics provided validation for the unexpected linkage between two entirely disparate branches of mathematics.

Following the release of the star-studded mystery thriller “The Number 23” in 2007, a significant number of individuals began to perceive occurrences of the titular number in various aspects of their lives. I was a student at the time, and some of my peers would react with unease whenever the number 23 made an appearance. This phenomenon, often referred to as the “frequency illusion” or the Baader-Meinhof phenomenon, intrigued many, as it illustrated how paying closer attention to a specific element, such as a number, could lead to a heightened perception of its presence.
For a considerable period, there was speculation that the late mathematician John McKay experienced a similar phenomenon, fixating on the number 196,884. McKay’s encounter with this number occurred in 1978 while he was exploring a mathematical paper unrelated to his primary field of study. Despite being immersed in geometry, McKay stumbled upon a sequence of numbers within number theory, beginning with 196,884.
This figure sparked familiarity in McKay due to his previous work on a theoretical mathematical entity known as the “monster.” This complex structure aimed to describe the symmetries of a geometric object residing in 196,883 dimensions, only one dimension fewer than the number 196,884. McKay’s discovery of this number seemed serendipitous, as he connected it to the dimensions of the monster structure: 196,883 + 1 = 196,884.
Although McKay’s findings initially garnered little attention from experts who attributed it to coincidental numerical similarities within diverse mathematical contexts, McKay persisted in his belief that geometry and number theory could be intertwined. He even sported T-shirts inscribed with the equation “196,883 + 1 = 196,884” at academic gatherings.
Subsequently, mathematician John Thompson’s exploration supported McKay’s suspicions by establishing a link between higher dimensions of the monster’s symmetries and subsequent numbers in the number theory sequence. Thompson’s calculations revealed a surprising correlation, reinforcing the possibility of a connection between seemingly disparate mathematical domains.
This revelation piqued the interest of the mathematical community, leading to further investigation into the potential link between geometry and number theory. Despite initial skepticism, the concept of “monstrous moonshine,” as termed by mathematicians John Conway and Simon Norton, gained traction as evidence of numerical patterns emerged, suggesting a deeper connection between these mathematical realms.
The theoretical prediction of the monster structure within group theory, resembling a periodic table for finite symmetries, further fueled this inquiry. With nearly all finite groups categorized into 18 classes and 26 outliers, the concept of the monster challenged conventional mathematical understanding, hinting at profound connections yet to be fully comprehended.
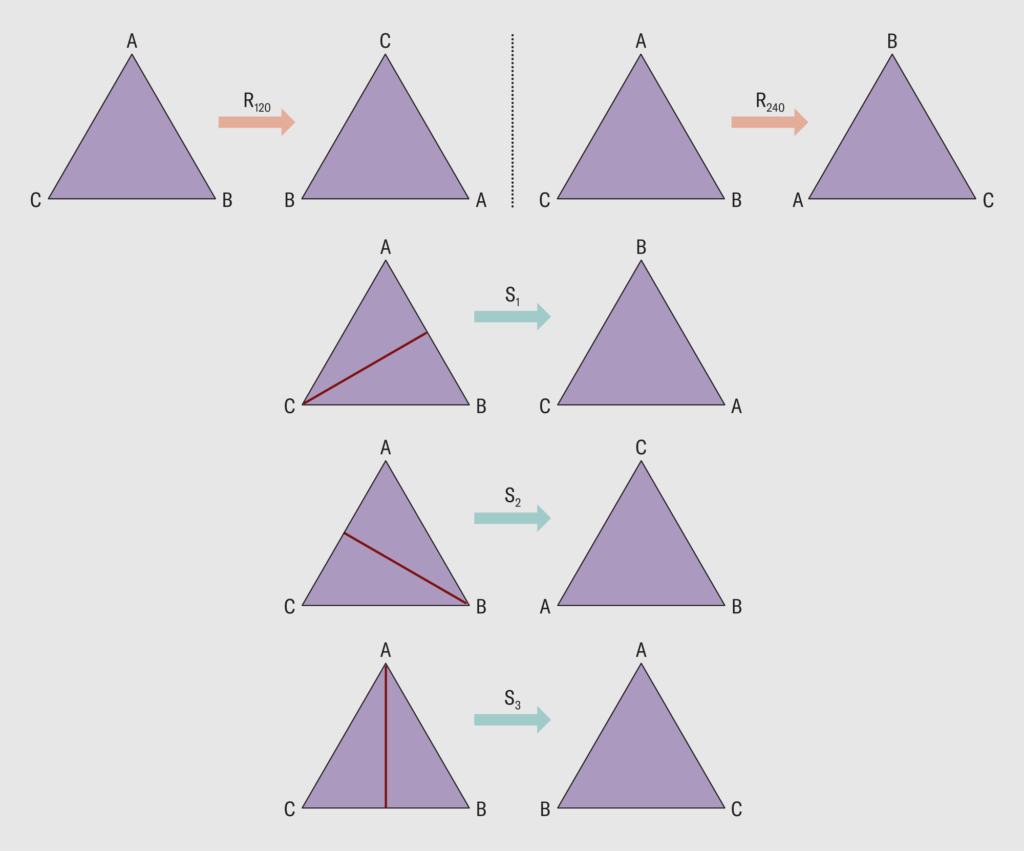
The initial outlier among these groups was the “monster,” foreseen by mathematicians Bernd Fischer and Robert Griess in 1973. The moniker derives from the immense scale of this group, boasting over 8 x 10^53 symmetries. To put this into perspective, consider that the symmetry group of a 20-sided “D20” die, or icosahedron, comprises only 60 symmetries, indicating that there are merely 60 conceivable transformations (rotations or reflections) that can be executed without altering the D20’s orientation.
Due to its immense scale, the monster posed significant challenges for mathematicians. “Most people thought it was going to be hopeless to construct it since much, much, much smaller groups required computer constructions at that time,” Borcherds explained in his YouTube video. Even powerful computers struggled with a structure consisting of 8 x 10^53 elements.
However, this pessimistic outlook was ultimately proven incorrect. In 1980, Griess successfully constructed the monster, thereby proving its existence—without the aid of computers.
Number theory primarily deals with integers, which may seem straightforward initially. However, to delve into the relationships between them, experts employ intricate concepts like modular forms. These functions, denoted as f(z), exhibit extreme symmetry. Similar to the sine function, understanding a specific segment of a modular form reveals its appearance across the entire function.
Modular forms are something like trigonometric functions, but on steroids,” mathematician Ken Ono told Quanta Magazine.
However, despite their complexity, modular forms play a pivotal role in mathematics. For instance, Andrew Wiles from the University of Oxford utilized them to prove Fermat’s Last Theorem, while Maryna Viazovska from the Swiss Federal Institute of Technology in Lausanne employed them to determine the densest sphere-packing arrangement in eight spatial dimensions. Due to the intricate nature of modular forms, they are often approximated by infinitely long polynomials, such as:
[ f(q) = \frac{1}{q} + 744 + 19,688q + 21,493,760q^2 + 864,299,970q^3 + \ldots ]
The prefactors preceding the variable ( q ) constitute a number sequence with intriguing properties from a number-theoretical perspective. McKay linked this number sequence with the monster group.
Borcherds first encountered the moonshine conjecture in the 1980s, recalling, “I was just completely blown away by this,” during an interview with YouTuber Curt Jaimungal. Sitting in one of Conway’s lectures at the time, Borcherds learned of the mysterious connection between number theory and group theory, a subject that captivated him thereafter. He embarked on a quest to uncover this suspected connection, eventually publishing his groundbreaking result in 1992, for which he received a Fields Medal six years later. His conclusion suggested that a highly speculative area of physics, string theory, could provide the missing link between the monster group and the number sequence.
String theory aims to unify the four fundamental forces of physics (electromagnetism, strong and weak nuclear forces, and gravity). Unlike conventional theories relying on particles or waves as the universe’s basic constituents, string theory involves one-dimensional structures resembling tiny vibrating threads, generating the familiar particles and interactions observed in the universe.
Borcherds recognized that string theory relied on numerous mathematical principles related to symmetries, including moduli. Closed strings oscillating through spacetime create two-dimensional tubes exhibiting the same symmetry as modular shapes, regardless of their oscillation patterns.
The specific type of string theory Borcherds explored could only be mathematically formulated in 25 spatial dimensions. While our observable universe comprises three visible spatial dimensions, string theorists presume the remaining 22 dimensions are compactified into tiny spheres or toroidal shapes. However, the physics hinges on their precise configuration, known as “compactification.”
Borcherds compactified 24 dimensions into a 24-dimensional toroidal surface and discovered that the associated string theory exhibited the symmetry of the monster group. The fact that only one free spatial dimension remained did not deter him, as he focused on the model’s mathematical properties rather than its applicability to our physical universe.
In this constructed framework, strings oscillate along the 24-dimensional torus, with the monster group dimensions representing the various vibration modes at different energy levels. Thus, at the lowest energy level, there is only one vibration mode, while at higher energy levels, there are 196,883 distinct possibilities, with the resultant trace exhibiting the symmetry of a modular form.
Borcherds successfully demonstrated the connection between the monster group and a modular form. This was not an isolated case; subsequently, mathematicians have linked other finite groups with various modular forms, with string theory serving as the conduit. Hence, even if string theory fails as a description of our universe, it can still unveil entirely new mathematical vistas.
Science
Why the Moon Turns Red: The Science Behind the Lunar Eclipse
On September 7, skywatchers across Asia, Africa, and Europe looked up to see the Moon slip from silver to dramatic red—a spectacular display that’s as much about Earth as it is about the Moon. Here’s why our Moon turns crimson every time a total lunar eclipse paints the sky.
What Actually Happens During a Total Lunar Eclipse?
A lunar eclipse occurs when the Earth moves precisely between the Sun and the Moon. While you might expect the Moon to disappear completely as it slips into Earth’s shadow, something far more beautiful happens: the Moon glows a deep red or orange, often called a “blood moon”.
This isn’t a rare magic trick. Lunar eclipses are a regular part of skywatching, but total eclipses—where the whole Moon is covered—are less common, occurring only a couple of times each year. The eclipse on September 7, 2025, is particularly notable for its long totality of 82 minutes and global visibility.
Why Does the Moon Look Red Instead of Black?
You’d think that when Earth blocks the Sun, the Moon would go entirely dark. Instead, it glows a haunting, coppery red. The explanation is pure science and a little bit of planetary teamwork.
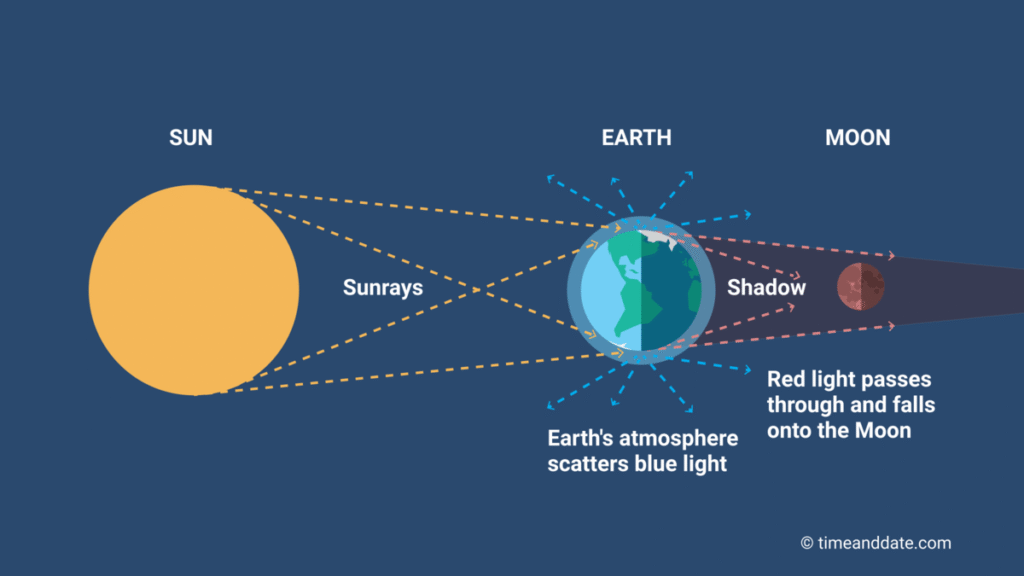
Earth’s Atmosphere Is the Secret Ingredient
As the Moon passes through the darkest part of Earth’s shadow—called the umbra—the only sunlight that reaches the Moon has traveled through Earth’s atmosphere first. This journey bends and filters the light, removing the shorter blue wavelengths and letting through the longer red and orange wavelengths.
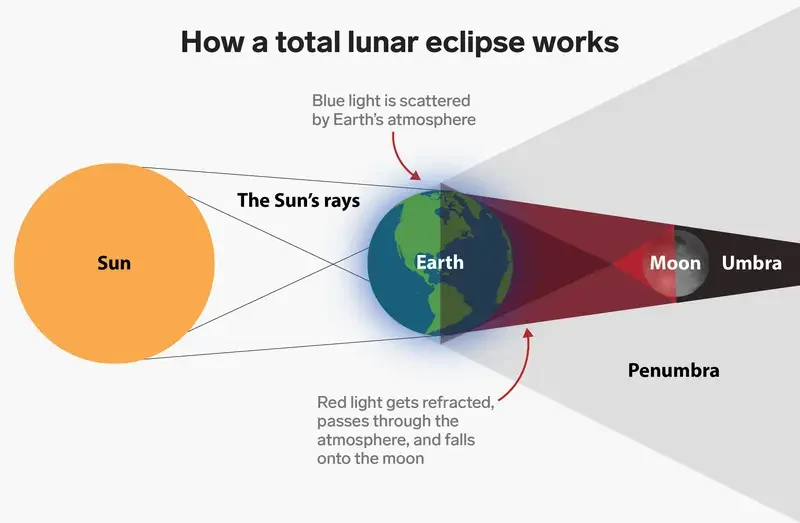
In other words, sunlight passes through a “ring” of Earth’s air. The bluer, shorter rays scatter (the same phenomenon that colors our daytime sky blue and sunsets orange/red), whereas the redder rays bend around the globe and spill onto the Moon’s surface. That’s why people all over the world see the Moon glowing red during the eclipse—it’s lit by every sunrise and sunset on Earth, all at once.
The Science: Rayleigh Scattering and Blood Moons
This filtering process is known as Rayleigh scattering—the same effect that gives us blue skies and those stunning red sunsets. When the Moon is inside the umbra, it catches sunlight that’s been bent through mammoth slabs of our planet’s air, with all the blue stripped out and only red and orange left to paint the lunar surface.
The term “blood moon” is popular, but not scientific. It’s just a poetic way of describing the result of this beautiful atmospheric chemistry.
Why the Color Varies Each Eclipse
Not every lunar eclipse looks the same. Sometimes the Moon shows a brighter orange; other times, it’s a dark rusty red. Volcanoes, wildfires, dust storms, and even local weather can all affect the clarity and color of the Earth’s shadow. For example, after a major volcanic eruption, there’s so much dust in the air that the Moon can appear an eerie, deep red or even brown.
A Universal Story in the Night Sky
One of the coolest things about a lunar eclipse is that it’s safe to watch with the naked eye—no fancy glasses needed! The next time you see the Moon turning red, remember: you’re looking at sunlight that’s passed through every sunrise and sunset on the planet, refracted and projected 380,000 km onto the Moon’s surface.
Fun Fact: If you were standing on the Moon during the eclipse, you’d see a ring of red light outlining Earth—a sight of all the sunsets and sunrises happening at that moment.
Science
Himachal Pradesh Declares Disaster Emergency: What Science Tells Us About the Himalayan Climate Crisis
With 300+ deaths and Rs 3,000 crore in damages, Himachal Pradesh just declared the entire state a disaster zone. But the real story isn’t just about this monsoon—it’s about how the Himalayas are fundamentally changing in ways that make tragedies like this the new normal.
This past week, Himachal Pradesh has declared its entire territory a ‘disaster-affected zone’ under the National Disaster Management Act, following unprecedented monsoon devastation across the state. The numbers behind this unprecedented decision are sobering: over 320 people dead, 1,337 roads blocked, and economic losses exceeding Rs 3,000 crores since June.

But here’s what the headlines aren’t telling you: this isn’t just about heavy rain. It’s about how climate change is rewiring one of the world’s most fragile mountain ecosystems, creating a perfect storm of geological instability, extreme weather, and human vulnerability.
The Scale of Devastation: By the Numbers
Let’s start with what’s happening right now. Since June 20, Himachal has been pummeled by what meteorologists are calling “extremely abnormal” weather patterns:
- 320+ deaths from landslides, flash floods, and weather-related accidents
- 1,280+ houses destroyed, with thousands more damaged
- 35,240 animals killed in the disasters
- Four national highways completely blocked
- 16 pilgrims died during the Manimahesh Yatra alone
The India Meteorological Department issued red alerts through September 2nd, predicting more “extremely heavy rainfall” of 200mm+ in single days. To put that in perspective, that’s more rain than many regions see in entire months.



The Science Behind the Chaos
What makes this particularly alarming isn’t just the intensity—it’s the pattern. Down to Earth magazine’s analysis shows the Himalayan region has experienced at least one disaster daily between January and August 2025. That’s not weather; that’s a fundamental shift in how this ecosystem functions.
Dr. Navin Juyal, a geologist who’s studied Himalayan flooding patterns for decades, explains what’s actually happening: “Climate change allows each kilogram of air to hold more moisture, so storms unload precipitation more intensely and erratically. In steep vertical valleys, even modest amounts of water can set deep moraines and loose slopes in motion”.
Here’s the key insight: the Himalayas are warming faster than the global average, creating what scientists call “atmospheric rivers”—narrow corridors of concentrated water vapor that can dump enormous amounts of precipitation in very short periods.
The Geological Time Bomb
But the weather is only half the story. The real danger lies in what’s happening beneath our feet.
Geologist S.P. Sati describes the mechanism: “In such steep, narrow valleys, a landslide at one point triggers similar processes in other glacial branches in rapid succession, resulting in multiple floods”.
Translation: the Himalayas are essentially a geological house of cards. When one slope fails, it creates a domino effect that can devastate entire river valleys.
The numbers are stark:
- 50% of natural springs across the Indian Himalayan Region are drying up
- Himalayan glaciers are retreating rapidly, increasing flood risks
- 1,072 sq km of forest cover lost between 2019-2021 in Himalayan states
- 110 glaciers lost in Arunachal Pradesh alone over 32 years
Human Choices, Natural Consequences
Here’s where the story gets complicated. While climate change is loading the dice, human decisions are determining how catastrophic the results become.
Take Dharali village in Uttarakhand, which was devastated by flash floods in early August. Satellite images show the entire market was built on what geomorphologists call a “debris-flow fan”—essentially, land formed by centuries of flood deposits.
“Establishing a settlement on land where the river continually deposits sediments is precarious,” says Wolfgang Schwanghart, a geomorphologist at the University of Potsdam who studies Himalayan disasters.
The pattern repeats across the region: construction on riverbeds, unauthorized buildings in landslide-prone areas, and infrastructure projects that alter natural drainage patterns without proper geological assessment.
The Broader Himalayan Crisis
Himachal’s disaster declaration comes as the entire Himalayan arc faces similar pressures. The region supports over 50 million people directly and provides water security for 600+ million through major river systems.
Key vulnerabilities by region:
- Ladakh: Glacier retreat and permafrost thaw
- Jammu & Kashmir: Frequent landslides along defense highways
- Uttarakhand: Erratic rainfall worsened by tourism pressure
- Sikkim: Transboundary glacial floods
- Arunachal Pradesh: Sudden river floods with inadequate warning systems
The 15th Finance Commission allocated Rs 1.6 lakh crore for climate resilience, but experts worry it’s not enough.
What This Means for the Future
Climate scientists are clear: this is the new normal, not an exception. Ashutosh Kumar from IIT Mandi explains: “Shorter, erratic bursts of weather—brief dry spells followed by intense moisture—mean slopes never fully dry out and therefore remain persistently weakened”.
The immediate priorities, according to experts:
- Moratorium on large projects in fragile zones until proper geological studies
- Real-time monitoring systems for dams, glacial lakes, and unstable slopes
- Community-specific early warning systems
- Dignified relocation for people in high-risk areas
The Uncomfortable Truth
Environmental campaigner Hemant Dhyani puts it bluntly: “The Himalayas must no longer be viewed as a source of revenue. You cannot justify destroying this natural treasure for short-term gains”.
But here’s the challenge: the same development projects causing geological instability are also providing jobs and economic opportunities for mountain communities. Finding sustainable alternatives isn’t just an environmental imperative—it’s an economic necessity.
Beyond Disaster Management
What’s happening in Himachal isn’t just a state emergency; it’s a preview of climate adaptation challenges across mountain regions worldwide. The solutions require thinking beyond traditional disaster response to fundamentally rethinking how humans live in rapidly changing mountain environments.
The science is clear: more intense rainfall, more unstable slopes, and more frequent disasters are now built into the Himalayan climate system. The question isn’t whether similar disasters will happen again—it’s whether we’ll learn to work with these new realities instead of being repeatedly surprised by them.
As one Dharali resident told rescuers: “We urged the administration to halt construction near the river, but nothing was done.” Now entire markets lie buried under 12 meters of debris.
The mountains are sending us a message. The question is whether we’re finally ready to listen.
What are your thoughts on balancing development needs with environmental protection in fragile mountain ecosystems? Have you experienced similar weather changes in your region?
Science
September Skywatch: Preview of All Celestial Highlights
Stock up on coffee, dust off those binoculars, and set your alarm—September’s sky calendar is absolutely stacked, and some of these events won’t come around again for years.
If you’re the kind of person who looks up at night just in case something magical’s happening, September is about to be your month. For seasoned stargazers, casual phone photographers, and everyone who’s just curious about what’s actually up there, here’s your guide to the most unmissable celestial events in September 2025.
Let’s face it: after a wild summer, we could all use a reason to stand outside at midnight and remember how cool the universe really is.
September’s Top Sky Events (Mark Your Calendar!)
Total Lunar Eclipse — September 7

Call your friends, grab your favorite snacks—this is the big one. On the 7th, India and much of Asia will get a front-row seat to a total lunar eclipse. The best part? It’s happening at a comfortable evening hour for most of us. The moon will turn that classic coppery “blood moon” red, and you don’t need any fancy gear—just clear skies and maybe a pair of binoculars to see craters in vivid detail. Don’t forget to make a wish. (I always do. Can’t prove it works, but hey—what if?)
- Peak Time (India): Around 8:45 PM IST
- How to Watch: Find a dark spot, give yourself about 30 minutes to adjust your eyes, and look up!
- Photographer Tip: Set your phone on Night Mode, brace against a wall, and you’ll get surprisingly good shots.
The Pleiades & A Rare Lunar Occultation — September 12

Star lore fans and night owls, this one’s for you. The Pleiades, often called the Seven Sisters, are a beautiful open star cluster in Taurus. On the night of the 12th, the moon will pass directly in front of (or “occult”) them. It’s a subtle, magical event that looks stunning through binoculars.
- Peak Time: Roughly 10-11 PM IST
- Where to Look: Towards the eastern sky, after moonrise
- Why It Matters: Lunar occultations of the Pleiades are rare and mesmerizing, like the universe is showing off just for you.
Saturn at Opposition — September 21
Saturn lovers, this is your night. When a planet’s at “opposition,” it’s closest to Earth and shines brightest for the year. Saturn will rise with the sun setting and is visible all night long—big, bright, and ringed. Even a small telescope or powerful binoculars should let you glimpse the rings, which never gets old.
- Pro Tip: Point your phone camera through the telescope eyepiece for easy astro-photography.
- Bonus: Look for Titan, Saturn’s largest moon, as a small pinprick of light nearby.
Equinox & Changing Seasons — September 23

Not as “wow” visually, but astronomically important. The autumnal equinox is when day and night are (basically) equal length all over the world. In India, this means the end of the rainy season and slightly cooler nights. The Milky Way is still visible overhead in the early evening, especially if you can get away from city lights.
Other Stealthy Sky Attractions
- Pre-dawn Venus: The “Morning Star” will be dazzling before sunrise all month.
- Orionids Meteor Shower (Early Preview): The real peak is in October, but you might spot a few early stragglers after midnight in the last week of September.
- ISS Flyovers: Check an app like Heavens-Above for when the International Space Station passes overhead—it moves fast and looks like a bright, steady “star” gliding by.
Pro Tips for First-Time Skywatchers
- App Up: Download a free sky map app (like Stellarium or SkySafari) and point your phone at the sky to ID stars and planets instantly.
- Red Flashlight: Use red cellophane on your torch if you’re night-watching; red light won’t wreck your night vision.
- Safety First: If you’re heading outside late, go with a friend and tell someone where you’re going. Snacks are highly recommended. 😉
- Photo Challenge: Tag your best snaps #SeptemberSkyWatch—there’s always a community eager to geek out with you.
Why September 2025 Is Special
Celestial events come in cycles, but combos like a total lunar eclipse and a rare star occultation in the same month? That’s a treat. Whether you’re making it a solo adventure, a family activity, or a date, September’s sky show has a little something for everyone.
In a world full of distractions, looking up is still the best kind of reset.
Let me know if you catch something amazing—or if you just want to share a blurry moon photo (we’ve all been there). Clear skies!










